基础概念
数据集是由数据组成的集合,数据质量越好价值也越高。
统计能够帮助我们:量化不确定性(quantify uncertainty)、辨别偏见(discern biases)。
需要考虑数据是哪里来的、是如何计算的,需要辨别哪些数据好、哪些数据不好,这些数据是做出决定的正确数据吗。
一手数据是自己从自然环境或实验中调查收集到的;二手数据就是现成的数据,从别人手里拿到的数据。
整理后的数据能够提供服务和方便、帮助做决定、有说服力、节省时间和金钱。
数据的中心(The Center of the Data)
平均值(Mean/Average)
数据的总和除以数据的个数。
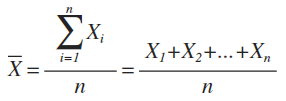
中位数(Median)
有相同数量的高于该点的数据和低于该点的数据,如果数据的个数是偶数个,Median 是中间两个数的平均值。
加权平均数(Weighted Mean)
将各数值乘以相应的权重,然后求和得到总体值,再除以总的权重和。
场景:课程总分由多部分构成,考试成绩、出勤情况、完成练习程度
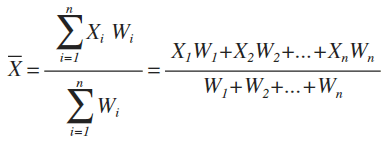
众数(Mode)
一组数据中出现最多的那个数,表示最有可能出现的数。
数据的变化性(Data Variability)
极差/范围误差/全距(Range)
数据集中最大值与最小值的差。
标准差/均方差(Standard Deviation)
标准差是离均值平方的算术平均数的平方根。标准差能反映一个数据集的离散程度,一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。方差是标准差的平方。
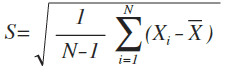
离群值(Outlier)
离群点是指一个数据集中,远离序列的一般水平的极端大值和极端小值。可通过表格和图标、标准差、z分数可以帮助我们识别离群点。
离群点没有明确的定义,离群点可以被认为是机会,它们是新趋势的开端。关于离群点,需要考虑这是一个真的离群点吗,它是怎么产生的,其中能学到什么,需要改进什么。
分布和相对位置(Distribution and Relative Position)
标准分数/z分数(Z-Score)
z分数是以标准差为单位度量原始分数离开平均数多少个标准差,正数表示大于平均数,负数表示小于平均数。
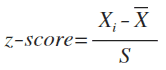
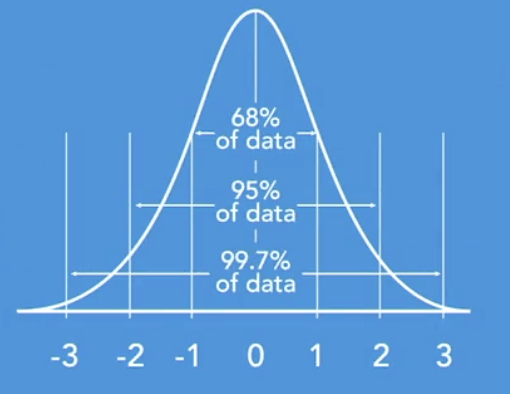
经验规则(Empirical Rule/Three Sigma Rule)
这里的 Sigma 代表标准差,作用于对称分布,对称分布通常用一个以均值为中心的钟形曲线。
经验规则是统计规律,指出了在正态分布,几乎所有数据都将落在均值的三倍标准差内。经验规则表明,68%的数据将分布在距离均值的一个标准差之内,95%的数据将分布在距离均值的两个标准差之内,99.7%的数据将分布在均值的三个标准偏差之内。
经验法则最常在统计中用于预测最后结果。在得到数据的标准差,并在可以收集确切的数据之前,该规则可作为一个对即将到来的数据的结果的粗略估计。该概率特别适用与一些需要消耗大量时间去收集的数据,或者甚至是不可能获得的数据。
百分位数(Percentile Rank)
将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数,可表示为:一组n个观测值按数值大小排列,如处于p%位置的值称第p百分位数,中位数是第50百分位数。第100百分位数是不可能的,因为那就是说你是班级中的前0%,既可以说你是班级的前1%,也可以说你是第99百分位数。
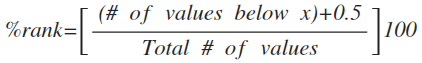
概率(Probability)
概率是事件发生的可能性,样本空间所有可能结果的概率之和一定是100%,概率分为客观概率和主观概率。客观概率是基于计算的,又分为:古典概率/事前概率,所有可能是已知的,并且出现概率相同,如投币;经验概率,特定的事件发生的次数占总体实验样本的比率,如估算任意一年的二月份中最低的日最高温度低于零度的概率,罚球命中率。主观概率没办法计算,无法重复,建立在过去的经验与判断的基础上,根据对未来事态发展的预测和历史统计资料的研究确定的概率,如解雇率。
多事件概率(Multiple Event Probability)
事件1/事件2出现的概率 = 事件1出现的概率 + 事件2出现的概率 - 事件1和事件2共同出现的概率。
条件概率,事件1已经发生的情况下,事件2出现的概率。两个事件 A 和 B 是独立的当且仅当 Pr(A∩B) = Pr(A)Pr(B)。
贝叶斯定理(Bayes theorem)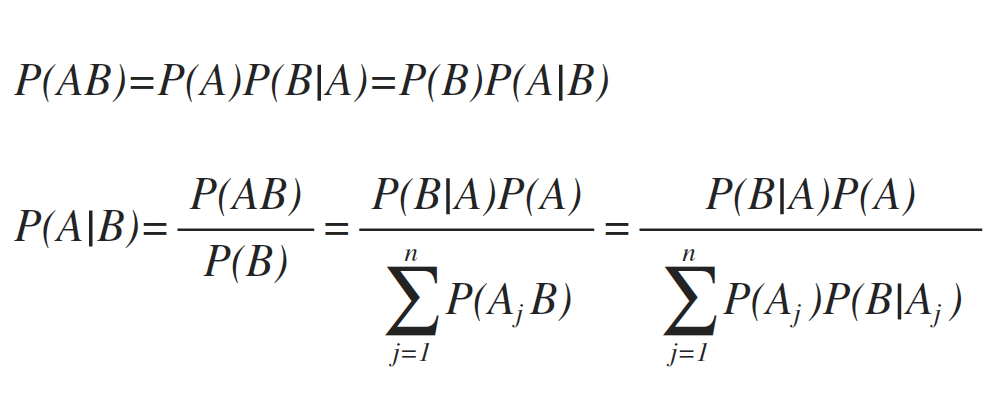
贝叶斯经典问题
Monty Hall problem: 出自美国的电视游戏节 Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。参赛者会看见三扇关闭的门,其中一扇的后面有辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门参赛者可以赢得汽车的概率是多少?
答案:简单的想选择当前门赢汽车的概率是1/3,选择另外两扇门赢汽车的概率是2/3,其中一扇已经打开了,换成另一个门赢汽车的概率就是2/3了。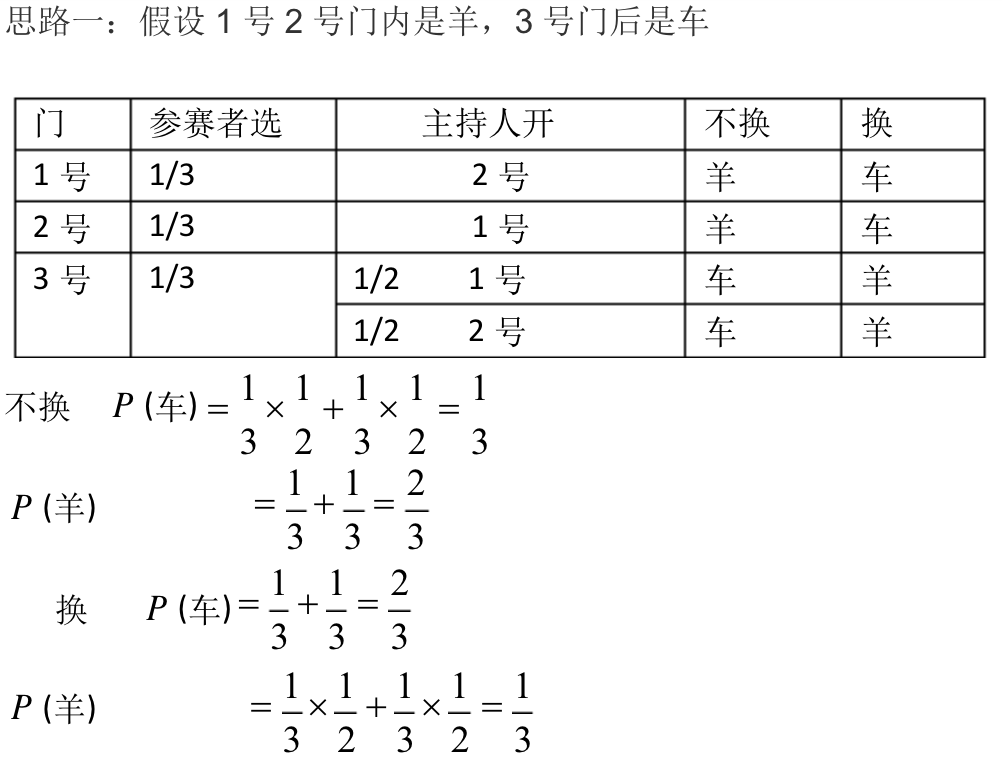
毒品检测问题。已知一家公司 0.5% 的员工吸毒。现在引入一个毒品检测的方式,对吸毒者检测为阳性的概率是 99%,非吸毒者检测出阳性的概率是 1%。已知一个公司的员工被检测出阳性,那么他吸毒的概率是多少?
答案:使用贝叶斯公式
事物是如何排列的(How Objects Are Arranged)
排列(Permutation)
总数为n,有序的排列,有多少可能 = n!
总数为n,选出有序的x个,有多少可能 = n! / (n - x)!
组合(Combination)
总数为n,选出无序的x个,有多少可能 = n! / [(n - x)! * x!]
离散与连续(Discrete VS. Continuous)
实验最终出现的结果是未知的、随机的,因此实验的结果叫做随机变量。随机变量表示随机试验各种结果的实值单值函数,随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。离散指的是有限多种可能性,自然数或整数计算。连续指的是有无限多种可能性,是某个区间内的任一实数。因为连续随机变量的取值有无限多种可能,因此需要使用一种替代的方式来计算这种类型的概率。
离散概率分布(Discrete Probability Distributions)

连续概率分布(Continuous Probability Distributions)
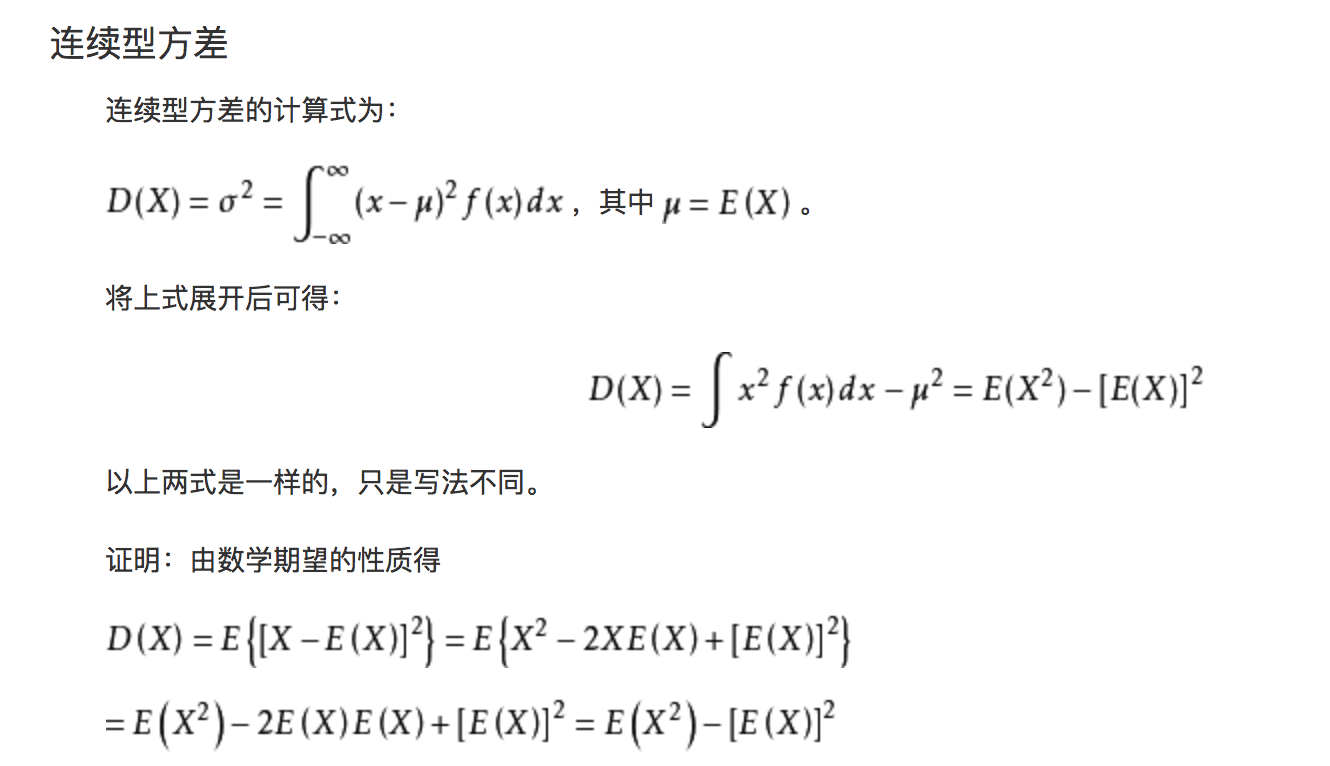

概率密度(Probability densities)
结果的可能是无限时,用曲线来描述结果的分布,这个曲线被叫做概率密度,曲线下的区域表示每种可能的结果。
钟形曲线(Bell-shaped curve)
正态分布。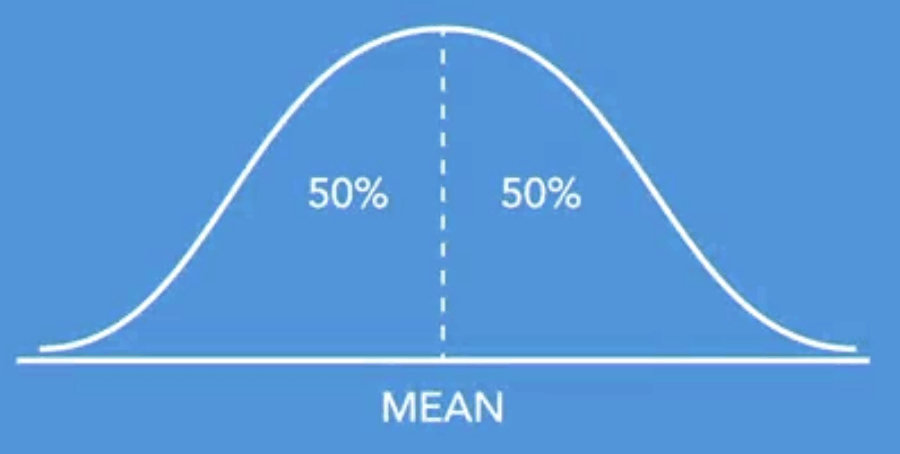
模糊中心极限定理(Fuzzy central limit theorem)
一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。